Inference and Validation
import torch
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
Here I'll create a model like normal, using the same one from my solution for part 4.
from torch import nn, optim
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.log_softmax(self.fc4(x), dim=1)
return x
The goal of validation is to measure the model's performance on data that isn't part of the training set. Performance here is up to the developer to define though. Typically this is just accuracy, the percentage of classes the network predicted correctly. Other options are precision and recall) and top-5 error rate. We'll focus on accuracy here. First I'll do a forward pass with one batch from the test set.
model = Classifier()
images, labels = next(iter(testloader))
# Get the class probabilities
ps = torch.exp(model(images))
# Make sure the shape is appropriate, we should get 10 class probabilities for 64 examples
print(ps.shape)
With the probabilities, we can get the most likely class using the ps.topk method. This returns the $k$ highest values. Since we just want the most likely class, we can use ps.topk(1). This returns a tuple of the top-$k$ values and the top-$k$ indices. If the highest value is the fifth element, we'll get back 4 as the index.
top_p, top_class = ps.topk(1, dim=1)
# Look at the most likely classes for the first 10 examples
print(top_class[:10,:])
Now we can check if the predicted classes match the labels. This is simple to do by equating top_class and labels, but we have to be careful of the shapes. Here top_class is a 2D tensor with shape (64, 1) while labels is 1D with shape (64). To get the equality to work out the way we want, top_class and labels must have the same shape.
If we do
equals = top_class == labels
equals will have shape (64, 64), try it yourself. What it's doing is comparing the one element in each row of top_class with each element in labels which returns 64 True/False boolean values for each row.
equals = top_class == labels.view(*top_class.shape)
Now we need to calculate the percentage of correct predictions. equals has binary values, either 0 or 1. This means that if we just sum up all the values and divide by the number of values, we get the percentage of correct predictions. This is the same operation as taking the mean, so we can get the accuracy with a call to torch.mean. If only it was that simple. If you try torch.mean(equals), you'll get an error
RuntimeError: mean is not implemented for type torch.ByteTensorThis happens because equals has type torch.ByteTensor but torch.mean isn't implement for tensors with that type. So we'll need to convert equals to a float tensor. Note that when we take torch.mean it returns a scalar tensor, to get the actual value as a float we'll need to do accuracy.item().
accuracy = torch.mean(equals.type(torch.FloatTensor))
print(f'Accuracy: {accuracy.item()*100}%')
The network is untrained so it's making random guesses and we should see an accuracy around 10%. Now let's train our network and include our validation pass so we can measure how well the network is performing on the test set. Since we're not updating our parameters in the validation pass, we can speed up the by turning off gradients using torch.no_grad():
# turn off gradients
with torch.no_grad():
# validation pass here
for images, labels in testloader:
...
Exercise: Implement the validation loop below. You can largely copy and paste the code from above, but I suggest typing it in because writing it out yourself is essential for building the skill. In general you'll always learn more by typing it rather than copy-pasting.
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
epochs = 30
steps = 0
train_losses, test_losses = [], []
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
optimizer.zero_grad()
log_ps = model(images)
loss = criterion(log_ps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
test_loss = 0
accuracy = 0
# Turn off gradients for validation, saves memory and computations
with torch.no_grad():
for images, labels in testloader:
log_ps = model(images)
test_loss += criterion(log_ps, labels)
ps = torch.exp(log_ps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor))
train_losses.append(running_loss/len(trainloader))
test_losses.append(test_loss/len(testloader))
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Training Loss: {:.3f}.. ".format(running_loss/len(trainloader)),
"Test Loss: {:.3f}.. ".format(test_loss/len(testloader)),
"Test Accuracy: {:.3f}".format(accuracy/len(testloader)))
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
plt.plot(train_losses, label='Training loss')
plt.plot(test_losses, label='Validation loss')
plt.legend(frameon=False)
Overfitting
If we look at the training and validation losses as we train the network, we can see a phenomenon known as overfitting.
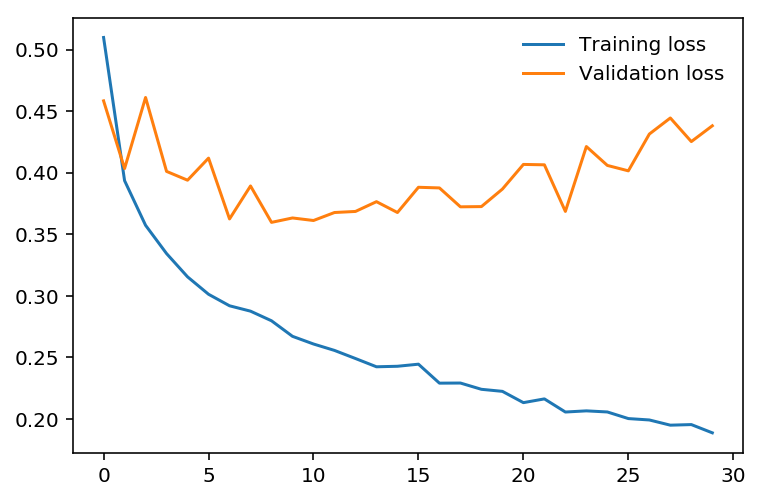
The network learns the training set better and better, resulting in lower training losses. However, it starts having problems generalizing to data outside the training set leading to the validation loss increasing. The ultimate goal of any deep learning model is to make predictions on new data, so we should strive to get the lowest validation loss possible. One option is to use the version of the model with the lowest validation loss, here the one around 8-10 training epochs. This strategy is called early-stopping. In practice, you'd save the model frequently as you're training then later choose the model with the lowest validation loss.
The most common method to reduce overfitting (outside of early-stopping) is dropout, where we randomly drop input units. This forces the network to share information between weights, increasing it's ability to generalize to new data. Adding dropout in PyTorch is straightforward using the nn.Dropout module.
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
# Dropout module with 0.2 drop probability
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
# Now with dropout
x = self.dropout(F.relu(self.fc1(x)))
x = self.dropout(F.relu(self.fc2(x)))
x = self.dropout(F.relu(self.fc3(x)))
# output so no dropout here
x = F.log_softmax(self.fc4(x), dim=1)
return x
During training we want to use dropout to prevent overfitting, but during inference we want to use the entire network. So, we need to turn off dropout during validation, testing, and whenever we're using the network to make predictions. To do this, you use model.eval(). This sets the model to evaluation mode where the dropout probability is 0. You can turn dropout back on by setting the model to train mode with model.train(). In general, the pattern for the validation loop will look like this, where you turn off gradients, set the model to evaluation mode, calculate the validation loss and metric, then set the model back to train mode.
# turn off gradients
with torch.no_grad():
# set model to evaluation mode
model.eval()
# validation pass here
for images, labels in testloader:
...
# set model back to train mode
model.train()
Exercise: Add dropout to your model and train it on Fashion-MNIST again. See if you can get a lower validation loss.
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
# Dropout module with 0.2 drop probability
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
# Now with dropout
x = self.dropout(F.relu(self.fc1(x)))
x = self.dropout(F.relu(self.fc2(x)))
x = self.dropout(F.relu(self.fc3(x)))
# output so no dropout here
x = F.log_softmax(self.fc4(x), dim=1)
return x
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
epochs = 30
steps = 0
train_losses, test_losses = [], []
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
optimizer.zero_grad()
log_ps = model(images)
loss = criterion(log_ps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
test_loss = 0
accuracy = 0
# Turn off gradients for validation, saves memory and computations
with torch.no_grad():
model.eval()
for images, labels in testloader:
log_ps = model(images)
test_loss += criterion(log_ps, labels)
ps = torch.exp(log_ps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor))
model.train()
train_losses.append(running_loss/len(trainloader))
test_losses.append(test_loss/len(testloader))
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Training Loss: {:.3f}.. ".format(train_losses[-1]),
"Test Loss: {:.3f}.. ".format(test_losses[-1]),
"Test Accuracy: {:.3f}".format(accuracy/len(testloader)))
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
plt.plot(train_losses, label='Training loss')
plt.plot(test_losses, label='Validation loss')
plt.legend(frameon=False)
# Import helper module (should be in the repo)
import helper
# Test out your network!
model.eval()
dataiter = iter(testloader)
images, labels = dataiter.next()
img = images[0]
# Convert 2D image to 1D vector
img = img.view(1, 784)
# Calculate the class probabilities (softmax) for img
with torch.no_grad():
output = model.forward(img)
ps = torch.exp(output)
# Plot the image and probabilities
helper.view_classify(img.view(1, 28, 28), ps, version='Fashion')